Classifier (introduction)¶
This notebook illustrates (on a very simple problem) how to use a classifier such as KNeighborsClassifier and SVM to separate two classes.
Let us do some imports as usual, we import pylab¶
%pylab inline
from matplotlib import rcParams
rcParams["figure.figsize"] = (10,6)
from sklearn.neighbors import KNeighborsClassifier
Populating the interactive namespace from numpy and matplotlib
The data¶
The data is made of two variables X1 and X2. THere are two classes defined by :
- X2 > 0.5
X2 <=0.5
X1 is uniformly distributed between 0 and 1
- X2 is uniformly distributed between 0 and 1
# create a data set
N = 50
X1_training = np.random.uniform(size=N)
X2_training = np.random.uniform(size=N)
training = np.vstack([X1_training, X2_training]).transpose()
# This defines the true label of the training
training_labels = X2_training > 0.5
# Create a test set
X1_test = np.random.uniform(size=5000)
X2_test = np.random.uniform(size=5000)
test = np.vstack([X1_test, X2_test]).transpose()
# This defines the true label of the training
test_labels = X2_test > 0.5
def plot_data(data, mask, score=None,):
plot(data[mask,0], data[mask, 1], "or")
plot(data[mask==False, 0], data[mask==False, 1], "ob")
if score:
title("Accuracy {}".format(score))
xlabel("X1", fontsize=20)
ylabel("X2", fontsize=20)
axhline(0.5, lw=4, alpha=0.5)
Visualise the training data¶
plot_data(training, training_labels)
Nearest Neighbours classification¶
Neighbors-based classification is computed from a simple majority vote of the nearest neighbors of each point: a query point is assigned the data class which has the most representatives within the nearest neighbors of the point.
scikit-learn implements two different nearest neighbors classifiers:
- KNeighborsClassifier implements learning based on the k nearest neighbors of each query point, where k is an integer value specified by the user.
- RadiusNeighborsClassifier implements learning based on the number of neighbors within a fixed radius r of each training point, where r is a floating-point value specified by the user.
The k-neighbors classification in KNeighborsClassifier is the more commonly used of the two techniques.
The optimal choice of the value k is highly data-dependent: in general a larger k suppresses the effects of noise, but makes the classification boundaries less distinct.
Fit a model¶
# build the model from the training data
model = KNeighborsClassifier()
model.fit(training, training_labels)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=5, p=2,
weights='uniform')
Score on the training data¶
score = model.score(training, training_labels)
score
0.93999999999999995
Performance on the test set¶
model.score(test, test_labels)
0.9698
subplot(1,2,1)
plot_data(training, training_labels, score)
# score on the test set.
score2 = model.score(test, test_labels)
subplot(1,2,2)
plot_data(test, model.predict(test), score2)
axhline(0.5, lw=3, color="k")
subplot(1,2,1)
xx, yy = np.meshgrid(linspace(0,1,20), linspace(0,1,20))
model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
contourf(xx, yy, Z, alpha=0.4)
<matplotlib.contour.QuadContourSet at 0x7f06ee496a90>
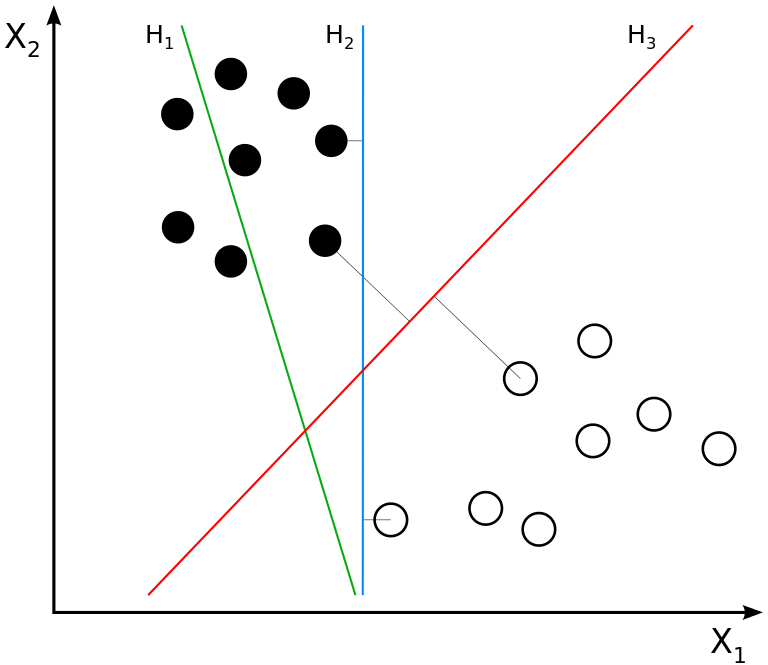
Support Vector Machines¶
Support vector machines (SVMs) are used for classification, regression and outliers detection.
The advantages of support vector machines are:
- Effective in high dimensional spaces even in cases where number of dimensions is greater than the number of samples.
- Uses a subset of training points in the decision function (called support vectors), so it is also memory efficient.
- Versatile: different Kernel functions can be specified for the decision function.
The disadvantages of support vector machines include:
- If the number of features is much greater than the number of samples, the method is likely to give poor performances.
- SVMs do not directly provide probability estimates, these are calculated using an expensive five-fold cross-validation (see Scores and probabilities, below).
from sklearn import svm
model = svm.SVC(kernel="linear", degree=1)
model.fit(training, training_labels)
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0, decision_function_shape=None, degree=3, gamma='auto', kernel='linear', max_iter=-1, probability=False, random_state=None, shrinking=True, tol=0.001, verbose=False)
score = model.score(training, training_labels)
score
1.0
pred = model.predict(test)
score2 = model.score(test, test_labels)
score2
0.98980000000000001
subplot(1,2,1)
plot_data(training, training_labels, score)
score2 = model.score(test, test_labels)
subplot(1,2,2)
plot_data(test, model.predict(test), score)
axhline(0.5, lw=3, color="k")
subplot(1,2,1)
xx, yy = np.meshgrid(linspace(0,1,20), linspace(0,1,20))
model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
contourf(xx, yy, Z, alpha=0.4)
<matplotlib.contour.QuadContourSet at 0x7f06fc220908>
Exercises¶
- change the kernel from linear to rbf or to poly
- Change N to 40 ot 400 and see impact on scores and classification